


Pictures (c) by Carlo Borer.
In previous posts I reported about the design and fabrication process of this piece of art.
Art, Design, Architecture, & Technology














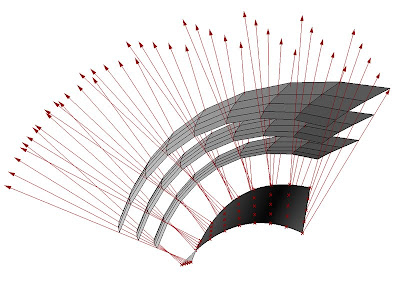
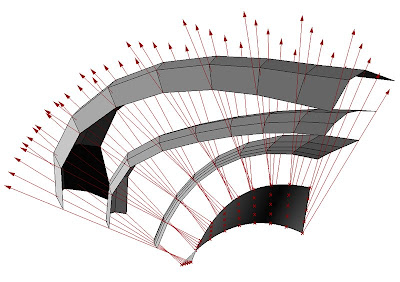



 Based on TNA, I implemented together with Philippe Block a grasshopper definition for the generation of structural freeform vaults. The image shows a structural surface with an non-uniform force distribution. This work is part of a resarch project done at the ETH Zurich.
Based on TNA, I implemented together with Philippe Block a grasshopper definition for the generation of structural freeform vaults. The image shows a structural surface with an non-uniform force distribution. This work is part of a resarch project done at the ETH Zurich.
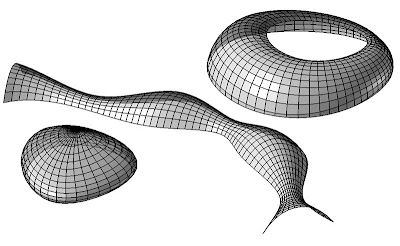
 A grasshopper definition for developable surface strips. Download here. Mårten Nettelbladt gives a nice description of developable surface types.
A grasshopper definition for developable surface strips. Download here. Mårten Nettelbladt gives a nice description of developable surface types.
 Gehry's east river guggenheim project in NYC. The use of flexible sheet material like paper in physical models generates developable geometries.
Gehry's east river guggenheim project in NYC. The use of flexible sheet material like paper in physical models generates developable geometries. Dennis Shelden, CTO at gt, describes in his phd thesis several ways to compute developable surfaces. Fig. (c) by Dennis Shelden.
Dennis Shelden, CTO at gt, describes in his phd thesis several ways to compute developable surfaces. Fig. (c) by Dennis Shelden. Museum MARTa in Herford, Germany. Most of the roof surfaces are developable. Geometric modelling of the roof construction has been done by Jess Maertterer. Further discription on his page.
Museum MARTa in Herford, Germany. Most of the roof surfaces are developable. Geometric modelling of the roof construction has been done by Jess Maertterer. Further discription on his page.



 Discovered by Rob Kusner, Director of the Center for Geometry, Analysis, Numerics and Graphics (GANG). The Kusner surface is an inversion of the Boy surface. The three discs are planes "reaching infinity".
Discovered by Rob Kusner, Director of the Center for Geometry, Analysis, Numerics and Graphics (GANG). The Kusner surface is an inversion of the Boy surface. The three discs are planes "reaching infinity".


 In topology, a smooth deformation from one surface in an other is called homotopy. The parameterization of this homotopy can be found on wolfram's page.
In topology, a smooth deformation from one surface in an other is called homotopy. The parameterization of this homotopy can be found on wolfram's page. A proposal for a pavillion by Christophe Delsart and Yvan Ngnodjom based on the boy surface for the ARPAM project.
A proposal for a pavillion by Christophe Delsart and Yvan Ngnodjom based on the boy surface for the ARPAM project.


 Download the definition here
Download the definition here
 This pentagonal tesselationis called cairo tiling.
This pentagonal tesselationis called cairo tiling. Extension of the congress center Davos, currently under construction. The roof structure is based on the cairo tesselation. By Degelo Architekten, Engineer: Dr. Schwartz Consulting
Extension of the congress center Davos, currently under construction. The roof structure is based on the cairo tesselation. By Degelo Architekten, Engineer: Dr. Schwartz Consulting Download the definition here.
Download the definition here.  The RGB chanels ploted as surface
The RGB chanels ploted as surface The input image
The input image This VB script component reads the RGB values from a jpeg file
This VB script component reads the RGB values from a jpeg file At digital matters, Tobias Wallisser from LAVA presented his Superformula Tower concept. Inspired by this beautiful idea, I created a grasshopper definition for towers based on a simpler formula.
At digital matters, Tobias Wallisser from LAVA presented his Superformula Tower concept. Inspired by this beautiful idea, I created a grasshopper definition for towers based on a simpler formula. Created with gifery.com
Created with gifery.com